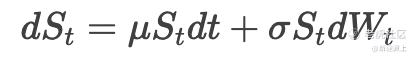社区

金融市场中，价格波动如同一场永不停歇的“舞蹈”，这场舞蹈的核心节奏却充满不确定性。19世纪初，英国植物学家罗伯特·布朗通过显微镜观察到花粉微粒在液体中的无规则运动，这一现象被称为布朗运动。看似微小的物理现象，却在百年后成为金融学中刻画市场随机性的核心工具。从股票价格波动到期权定价，从风险管理到资产配置，布朗运动及其衍生模型为金融市场的复杂性提供了数学描述，既满足了理论严谨性，又为实践提供了可操作的框架。

一、布朗运动的基本概念与金融映射

标准布朗运动（Wiener Process）是一种连续时间随机过程，核心特征包括：独立增量性（未来变化与历史无关）、正态分布性（变化幅度服从正态分布）、连续路径性（无跳跃波动）。这些特性与金融市场的某些规律高度契合——例如，股票价格的未来走势通常被认为与历史路径无关，而短期波动往往呈现近似正态分布。

若将金融市场比作一间暗室，布朗运动则像是一束光，照亮了价格随机性的本质。诺贝尔经济学奖得主保罗·萨缪尔森曾说：“金融市场没有记忆”。这句话正是对布朗运动独立增量性的生动诠释。

二、几何布朗运动：从物理到金融的跃迁

单纯的标准布朗运动允许数值为负，而资产价格不可能为负，因此金融学家引入了几何布朗运动（GBM）。数学表达为：

St 为资产价格，μ 为预期收益率，σ 为波动率，Wt 为标准布朗运动。这一模型的核心优势在于：

1. 非负性：价格始终为正

2. 比例波动：波动幅度与价格成正比，符合市场实际

例如：一只股价为100元的股票，每日涨跌幅度可能为1%，当股价升至200元时，波动比例仍维持1%左右。几何布朗运动通过随机微分方程（SDE）捕捉了这一特性，成为布莱克-舒尔斯期权定价模型的基石。

三、金融应用：从期权定价到风险控制

1. 期权定价的“革命”

1973年，布莱克、舒尔斯与默顿基于几何布朗运动提出期权定价模型（BS模型），彻底改变了衍生品市场。该模型假设股票价格服从GBM，通过伊藤引理推导出期权价格的偏微分方程，最终给出欧式期权的闭式解。例如，若某股票现价为100元，波动率为20%，无风险利率为3%，则可通过BS公式计算出一年后行权价为110元的看涨期权合理价格约为8.2元。这一模型至今仍是场内期权交易的核心工具。

2. 风险度量的“标尺”

在银行理财与投资管理中，布朗运动被用于模拟市场风险。例如，通过蒙特卡洛模拟生成资产价格的数千条GBM路径，可估算投资组合的在险价值（VaR）。中国银行间市场交易商协会的研究表明，基于布朗运动的风险模型能有效识别理财产品在极端市场条件下的潜在亏损。

3. 资产配置的“指南”

现代投资组合理论（MPT）假设资产收益服从正态分布，这一假设隐含了布朗运动的逻辑。通过布朗运动驱动的随机过程，投资者可动态调整股票、债券等资产的权重，以平衡收益与风险。

四、局限性与前沿发展

尽管布朗运动应用广泛，但其假设存在“理想化”成分：

• 肥尾效应：实际市场中极端事件（如股灾）频率高于正态分布预测

• 波动率微笑：BS 模型假设波动率为常数，现实中波动率随时间与价格变化

学者提出改进模型，如引入跳扩散过程、G-布朗运动等。例如，G-布朗运动通过不确定波动率框架，更灵活地刻画金融风险系统的渐近行为。此外，半鞅理论进一步证明，超越布朗运动的模型可能引入套利机会，从而为市场有效性提供数学解释

五、结语：随机中的秩序

布朗运动如同金融市场的“基因片段”，将看似混沌的价格波动转化为可量化的数学语言。从爱因斯坦对分子运动的物理解释，到现代金融衍生品的万亿市场，这一工具的演化体现了跨学科的智慧交融。尽管未来模型会更复杂，但布朗运动作为基础范式，始终是理解金融随机性的第一把钥匙。正如华尔街格言所言：“市场总是正确的，但它的正确性藏在随机的面纱之下”。揭开这层面纱，正是布朗运动赋予金融学的力量。

@小虎征文